Ctrl+K
Ctrl+K

Coupled Problems - Monolithic Approach#

Problem Formulation#

In this demo we show how cashocs can be used with a coupled PDE constraint. For this demo, we consider a monolithic approach, whereas we investigate an approach based on a Picard iteration in Coupled Problems - Picard Iteration.

As model example, we consider the following problem

\[\begin{split} \begin{align} &\min\; J((y,z),(u,v)) = \frac{1}{2} \int_\Omega \left( y - y_d \right)^2 \text{ d}x + \frac{1}{2} \int_\Omega \left( z - z_d \right)^2 \text{ d}x + \frac{\alpha}{2} \int_\Omega u^2 \text{ d}x + \frac{\beta}{2} \int_\Omega v^2 \text{ d}x \\ &\text{ subject to }\qquad \begin{alignedat}[t]{2} -\Delta y + z &= u \quad &&\text{ in } \Omega, \\ y &= 0 \quad &&\text{ on } \Gamma,\\ -\Delta z + y &= v \quad &&\text{ in } \Omega,\\ z &= 0 \quad &&\text{ on } \Gamma. \end{alignedat} \end{align} \end{split}\]

In constrast to Using Multiple Variables and PDEs, the system is now two-way coupled. To solve it, we employ a mixed finite element method in this demo.

Implementation#

The complete python code can be found in the file demo_monolithic_problems.py and the corresponding config can be found in config.ini.

Initialization#

The initialization for this example works as before, i.e., we use

from fenics import *

import cashocs

config = cashocs.load_config("config.ini")
mesh, subdomains, boundaries, dx, ds, dS = cashocs.regular_mesh(50)

For the mixed finite element method we have to define a fenics.MixedFunctionSpace, via

elem_1 = FiniteElement("CG", mesh.ufl_cell(), 1)
elem_2 = FiniteElement("CG", mesh.ufl_cell(), 1)
V = FunctionSpace(mesh, MixedElement([elem_1, elem_2]))

The control variables get their own fenics.FunctionSpace

U = FunctionSpace(mesh, "CG", 1)

Then, the state and adjoint variables state and adjoint are defined

state = Function(V)
adjoint = Function(V)

As these are part of a fenics.MixedFunctionSpace, we can access their individual components by

y, z = split(state)
p, q = split(adjoint)

Similarly to Using Multiple Variables and PDEs, p is the adjoint state corresponding to y, and q is the one corresponding to z.

We then define the control variables as

u = Function(U)
v = Function(U)
controls = [u, v]

Note, that we directly put the control variables u and v into a list controls, which implies that u is the first component of the control variable, and v the second one.

Hint

An alternative way of specifying the controls would be to reuse the mixed function space and use

controls = Function(V)
u, v = split(controls)

Although this formulation is slightly different (it uses a fenics.Function for the controls, and not a list) the de-facto behavior of both methods is completely identical, just the interpretation is slightly different (since the individual components of the fenics.FunctionSpace V are also CG1 functions).

Definition of the mixed weak form#

Next, we define the mixed weak form. To do so, we first define the first equation and its Dirichlet boundary conditions

e_y = inner(grad(y), grad(p)) * dx + z * p * dx - u * p * dx
bcs_y = cashocs.create_dirichlet_bcs(V.sub(0), Constant(0), boundaries, [1, 2, 3, 4])

and, in analogy, the second state equation

e_z = inner(grad(z), grad(q)) * dx + y * q * dx - v * q * dx
bcs_z = cashocs.create_dirichlet_bcs(V.sub(1), Constant(0), boundaries, [1, 2, 3, 4])

To arrive at the mixed weak form of the entire syste, we have to add the state equations and Dirichlet boundary conditions

e = e_y + e_z
bcs = bcs_y + bcs_z

Note, that we can only have one state equation as we also have only a single state variable state, and the number of state variables and state equations has to coincide, and the same is true for the boundary conditions, where also just a single list is required.

Defintion of the optimization problem#

The cost functional can be specified in analogy to the one of Using Multiple Variables and PDEs

y_d = Expression("sin(2*pi*x[0])*sin(2*pi*x[1])", degree=1)
z_d = Expression("sin(4*pi*x[0])*sin(4*pi*x[1])", degree=1)
alpha = 1e-6
beta = 1e-6
J = cashocs.IntegralFunctional(
    Constant(0.5) * (y - y_d) * (y - y_d) * dx
    + Constant(0.5) * (z - z_d) * (z - z_d) * dx
    + Constant(0.5 * alpha) * u * u * dx
    + Constant(0.5 * beta) * v * v * dx
)

Finally, we can set up the optimization problem and solve it

optimization_problem = cashocs.OptimalControlProblem(
    e, bcs, J, state, controls, adjoint, config=config
)
optimization_problem.solve()

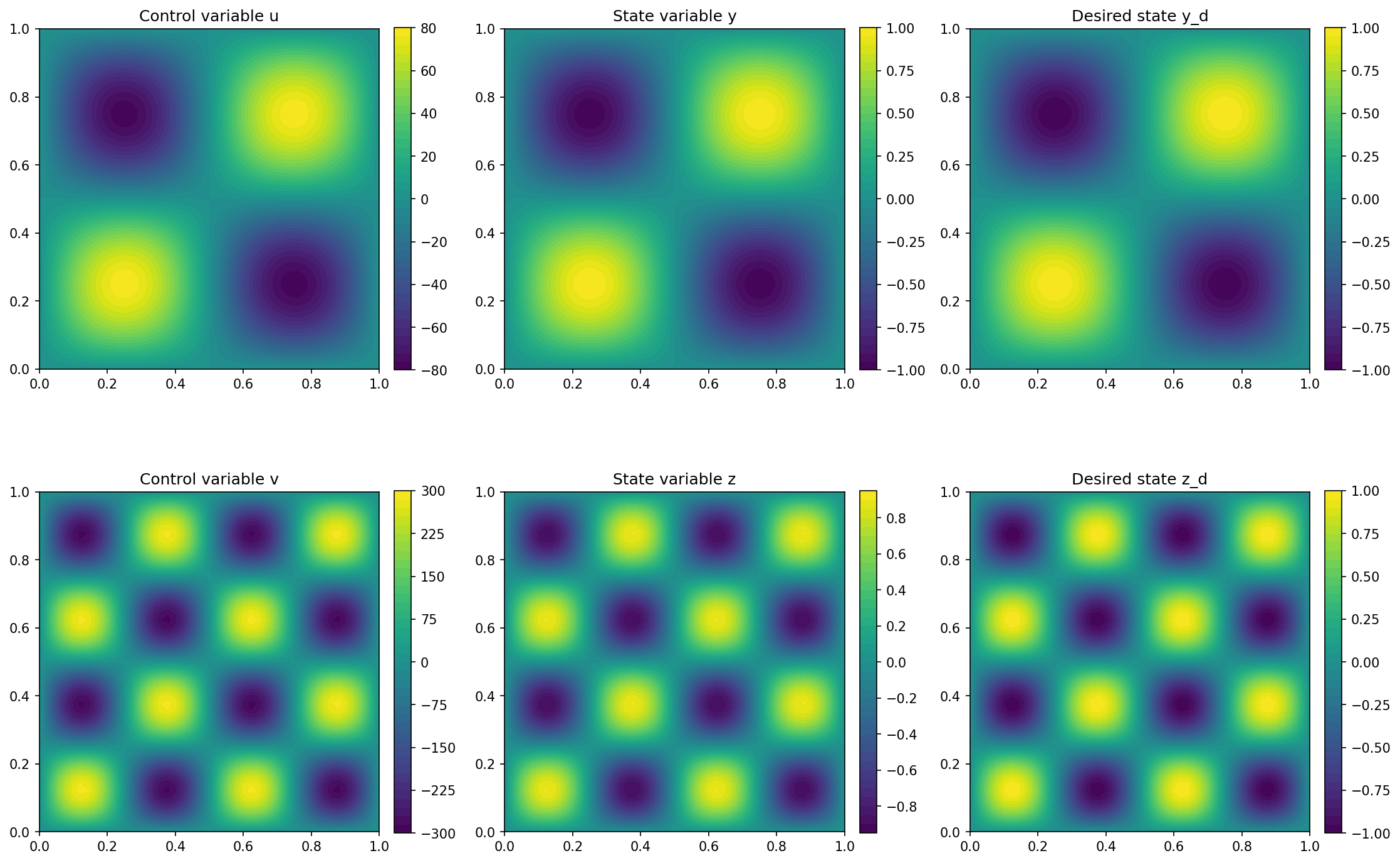
We visualize the result with the code

y, z = state.split(True)
import matplotlib.pyplot as plt

plt.figure(figsize=(15, 10))

plt.subplot(2, 3, 1)
fig = plot(u)
plt.colorbar(fig, fraction=0.046, pad=0.04)
plt.title("Control variable u")

plt.subplot(2, 3, 2)
fig = plot(y)
plt.colorbar(fig, fraction=0.046, pad=0.04)
plt.title("State variable y")

plt.subplot(2, 3, 3)
fig = plot(y_d, mesh=mesh)
plt.colorbar(fig, fraction=0.046, pad=0.04)
plt.title("Desired state y_d")

plt.subplot(2, 3, 4)
fig = plot(v)
plt.colorbar(fig, fraction=0.046, pad=0.04)
plt.title("Control variable v")

plt.subplot(2, 3, 5)
fig = plot(z)
plt.colorbar(fig, fraction=0.046, pad=0.04)
plt.title("State variable z")

plt.subplot(2, 3, 6)
fig = plot(z_d, mesh=mesh)
plt.colorbar(fig, fraction=0.046, pad=0.04)
plt.title("Desired state z_d")

plt.tight_layout()
# plt.savefig('./img_monolithic_problems.png', dpi=150, bbox_inches='tight')

so that the output should look like this

On this page
Show Source